x + y = k となるx, yの場合の数

本来解きたかったのは AtCoder のこの問題です。

解説 PDF も YouTube 解説もありますが、基礎というか前半部分で実装する x + y =k は頻出かなと思ったのでメモを残します。

問題文

$x, y, k \in \mathbb{Z}$ が $a \leq x \leq b, \quad c \leq y \leq d$を満たし、$k$を任意の定数としたとき、$x + y = k$となる場合の数を求めよ

２つの数直線を縦で足し合わせると常に$k$となるように噛み合わせる。

x の数直線は右が正、y の数直線は左が正となることに注意する。

以下のように色付けされた場所の長さが、求めたい場合の数である。

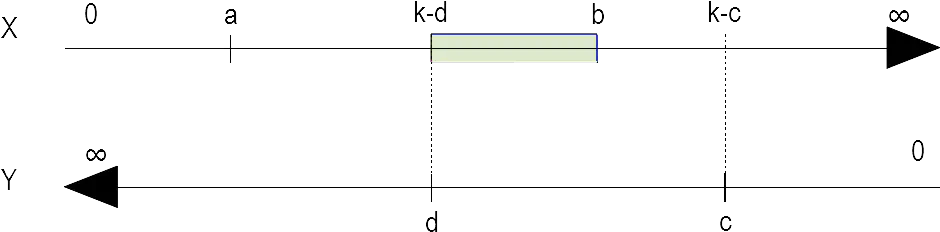
色付けされた部分の左側を$l$、右側を$r$とすると、

$$ \begin{eqnarray*} l &=& \text{max}(a, k-d)\\ r &=& \text{min}(b,k-c)\\ \end{eqnarray*} $$

$l,r$自身をあわせた範囲が答になるので、

$$r - (l - 1) = \text{min}(b, k-c) - \text{max}(a, k-d) + 1$$