WolframAlpha は Wolfram 言語に基づいているので、それを入れれば回答を得ることができる。

しかし Wolfram 言語の膨大なドキュメントをさかのぼっていてはいざというときすぐにたどり着けない。

大学 2 年まででよく使った（つかいそう）なのをここにまとめておくよ。

方程式

連立方程式や、n 次方程式、不等式などに使える。

$$ \left\{ \begin{align} ax + y &= 7\\ bx + y &= 1 \end{align}\right. $$

Solve[ax + y == 7 && bx + y == 1, x]

$$ ax^2 + bx +c =0$$

Solve[ax^2 + bx + c == 0, x]

$$ x^2 > y^2 $$

Solve[x^2 > y^2, x]

第 3 引数にはオプションを指定できる。

微分、微分方程式

通常の微分から、微分方程式まで解ける

$$\frac{dx^n}{dy}$$

D[x^n, x]

$$y’(x) + y(x) = a \sin{x}$$

DSolve[y'[x] + y[x] == a Sin[x], y[x], x]

積分 (定積分,不定積分)

$$\int x^n dx$$

Integrate[x^n, x]

$$\int_0^\infty \frac{1}{2^x}$$

Integrate[1/2^x, {x,0,\[Infinity]}]

その他の式

Sin, Cos

$$sin \theta$$

Sin[\Theta]

$$cos \theta$$

Cos[\Theta]

極限 limit

$$\lim_{x \to \infty} \frac{x+1}{x-1}$$

Limit[(x + 1)/(x - 1), x -> \[Infinity]]

総和 sum

$$\sum_{n=1}^10 n$$

NSum[n,1,10]

Log

$$\log_2{3}$$

Log[2, 3]

指数関数 e

$$e^{i \pi}$$

Exp[I Pi/5]

階乗 !

$$10!$$

Factorial[10]

組み合わせ、二項係数 Combination

$${}_{10} C_3$$

Binomial[10,3]

順列 Permulation

$${}_{5} P_2$$

Permutation[5,2]

記号、定数

便利な機能

図を描写 plot

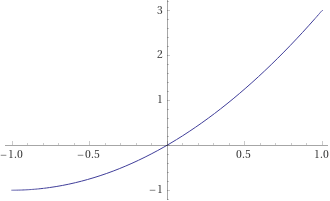
Plot[t^2 + 2t , {t, -1, 1}]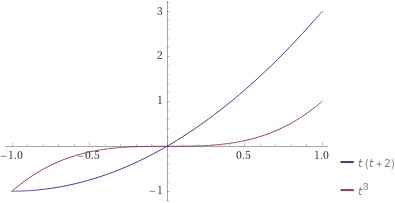

第 1 引数に複数の関数を入れて描写することもできる。

Plot[{t^2+2t, t^3},{t,-1,1}]

端書

また変数は入れ子にして使うことができる。何か一覧に追加してほしい等あれば、コメントでお知らせください。