問題
ABC194のD問題
[要約]n個の頂点のグラフがあり、最初は頂点1にいる。
一回の試行でランダムに頂点を選び連結にしていく。
すべての頂点を連結にするときの、試行回数の期待値を求める。
つまり、頂点すべてを一回以上訪れるまで平均して何回試行を行うかを求める問題。
勘違いと自問自答
「私の知らない知識が載っている、ほう」
確率\(p(p \neq 0)\)で成功する試行を、成功するまで行うときの試行回数(最後の成功した回も含む) の期待値は\(\frac{1}{p}\)である
https://atcoder.jp/contests/abc194/editorial/823
「そうか、期待値は確率の逆数なんだ！完全に理解した！」(←圧倒的早とちり）
「そしたらn個をすべて連結にする確率は、
$$\frac{n-1}{n} \times \frac{n-2}{n} \times \frac{n-3}{n} \times \cdots \times \frac{1}{n} = \frac{(n-1)!}{n^{n-1}}$$
で、期待値は\(\frac{n^{n-1}}{(n-1)!}\)！？！？」
もちろんこんなはずもなく、この固定観念に縛られなかなか抜け出せなかった。
解決に向けての間違い探し
唐突に導き出した、\(\frac{(n-1)!}{n^{n-1}}\)。これはもちろんすべてを連結にするときの確率だが、正確には「n-1回の試行回数で、n個の頂点すべてを連結にするときの確率」であって、
このマルコフモデルを最短でゴールまでたどりつくときの確率である。
本来ならばゴールにつくまでに、1,2,3,3,3,4,4,5,6,7,7,nのように同じところで何周も自己ループしたり、必ずどこかで道草を食うはず。
つまり、「n-1回の試行回数で、n個の頂点すべてを連結にするときの確率」を逆数にして「n個の頂点すべてを連結にするときの試行回数の期待値」などと騒ぎ立てるは圧倒的に間違っている！！！
(自問自答おわり)
解答編
n個の頂点のうち、すでに訪れた(連結)頂点の個数のマルコフモデルを考える。
ここで、それぞれの状態にいるとき、前のデータの影響を受けないことが大事。
例えば状態1から2になる時と状態2から3になる時は、互いに影響を与えることはないので、独立に考えることができる。
そして、頭をこんがらがらせるこの定理
確率\(p\)で起きる事象が起きるまでの試行回数の期待値は\(\frac{1}{p}\)
http://zakii.la.coocan.jp/enumeration/32_bernoulli_k.htm
abc194の問題のように状態が次から次へ変わっていく問題では落ち着いて考えることが必要。
あくまでこの定理は状態Aから状態Bに推移する、そのときのみに使える定理であってabc194の問題を考える時は、ステップごとに分けて考える。
ステップごとに考える(ステップ1)
まず、連結の大きさが1の状態から、連結の大きさが2である状態になる確率と期待値を求める
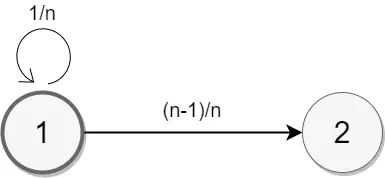
全体でn個ある頂点から、まだ訪れていない頂点n-1個を訪れる確率は\(\frac{n-1}{n}\)
そしてその期待値は、確率pで起きる事象が起きるまでの試行回数の期待値は\(1/p\)を使うと\(\frac{n}{n-1}\)
よって、状態1から状態2になるまで、平均して\(\frac{n}{n-1}\)回の試行を行えば次のステップへすすめる。
ステップ2
連結の大きさが2の状態から、連結の大きさが3である状態になる確率と期待値を求める
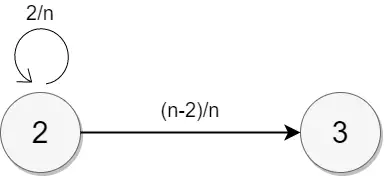
全体でn個ある頂点から、まだ訪れていない頂点n-2個を訪れる確率は\(\frac{n-2}{n}\)
そしてその期待値は、\(\frac{n}{n-2}\)
よって、状態2から状態3になるまで、平均して\(\frac{n}{n-2}\)回の試行を行えば次のステップへすすめる。
また、状態1から状態3になるまで、平均して\(\frac{n}{n-1} + \frac{n}{n-2}\)試行を行えば次のステップへすすめる。
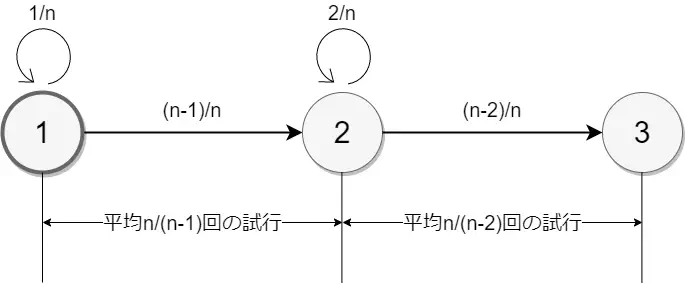
ステップi
連結の大きさがiの状態から、連結の大きさがi+1である状態になる確率と期待値を求める
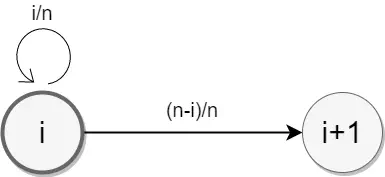
全体でn個ある頂点から、まだ訪れていない頂点n-i個を訪れる確率は\(\frac{n-i}{n}\)
そしてその期待値は、\(\frac{n}{n-i}\)
よって、状態iから状態i+1になるまで、平均して\(\frac{n}{n-i}\)回の試行を行えば次のステップへすすめる。
また、状態1から状態iになるまで、平均して\(\frac{n}{n-1} + \frac{n}{n-2} + \cdots + \frac{n}{n-i}\)試行を行えば次のステップへすすめる。
解答
以上のことから、状態1から状態nになるまでの操作回数の期待値は、平均して何回試行を行うかということに等しいので、
$$\frac{n}{n-1} + \frac{n}{n-2} + \cdots \frac{n}{1} = \sum_{i=1}^{n-1} \frac{n}{n-i}$$
コメント